Explore the fascinating world of phase transitions across physics and computer science in this comprehensive lecture. Delve into the universal nature of phase transitions, from classical examples like water state changes to their occurrence in neuroscience, biology, financial markets, and information processing systems. Discover the principle of minimum thermodynamic potential, mean-field models of imitation effects, and the Ising model for ferromagnetism. Investigate phase transitions in combinatorial optimization problems, including the Hamiltonian path and graph coloring. Examine the fundamental limits of communication through channel capacity and error-correction techniques. Gain insights into perceptron learning for classification and the broader implications of phase transitions in complex systems.
Phase Transitions - From Physics to Computer Science
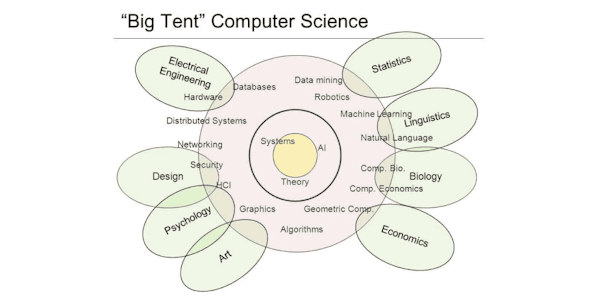
Overview
Syllabus
Phase transitions: from physics to computer science
Water phase diagram
A tiny bit of physics: principle of minimum of thermodynamic potential
Free energy potential: the perpetual tension between order and disorder...
Mean-field model of imitation effects
Ferromagnetism and Ising model
Vicsek model
Phase transitions in combinatorial optimisation
The seven bridges from Königsberg (1735)
Hamiltonian path problem: Can we find a path that encounters each NODE a SINGLE TIME?
3-colouring of random graphs
Phase transitions in communications: the birth of information theory
Fundamental limit to communication: channel capacity
Nucleation in error-correction: spatial coupling
Perceptron learning for classification
Taught by
ICTP Mathematics
