Explore a comprehensive lecture on the progress of computer-assisted mathematical proofs, from the four-color puzzle to the Kepler conjecture. Delve into how computer science and software engineering methods have been applied to mathematical language, leading to new insights like synthetic homotopy type theory. Examine various landmarks in computer proofs, including the Odd Order theorem and its implications for finite groups. Investigate the challenges and benefits of formalizing mathematical proofs, the development of proof algorithms, and the implementation of algebraic notation in digital formal texts. Learn about interactive mathematics, algebraic interfaces, and the emergence of Homotopy Type Theory. Gain insights into the future of computer-assisted mathematics and its potential to revolutionize mathematical research and education.
Georges Gonthier - Computer Proofs - Teaching Computers Mathematics, and Conversely
International Mathematical Union via YouTube
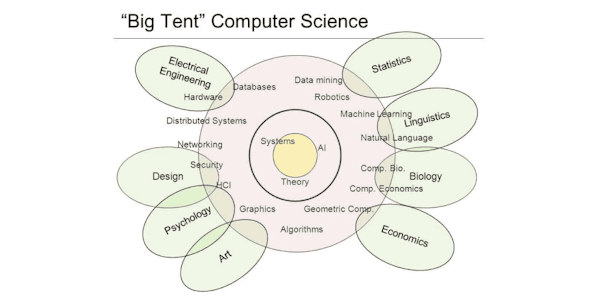
Overview
Syllabus
Intro
Is formalization a formality?
Some computer proof landmarks
An old puzzle's story
Saved by the computer?
The whole proof
Proof Algorithms
Reflecting reducibility
Building a square
Building configurations
Colouring interpretation
The Poincaré principle
Minimal logic
Functions in logic The Moderns
Crafting map descriptions
Proof by folklore
Size matters
The Odd Order Theorem
All finite groups of odd order are solvable. Proof: Let G be a minimal counter-example...
A mathematical library shelf
Textbook vs. digital formal text
Interactive Math
Algebraic Notation
Implementing notation
Algebra interfaces Equality
Inferring notation
Basic interfaces and objects bool
Ad hoc inference
Interfacing big operators
Coprime cycle coherence
A dot product matrix puzzle
An integer norm problem
Sorting a combinatorial mess
Homotopy type theory Type A
Synthetic Homotopy Type Theory
Cubical Type Theory
Conclusion
Taught by
International Mathematical Union
