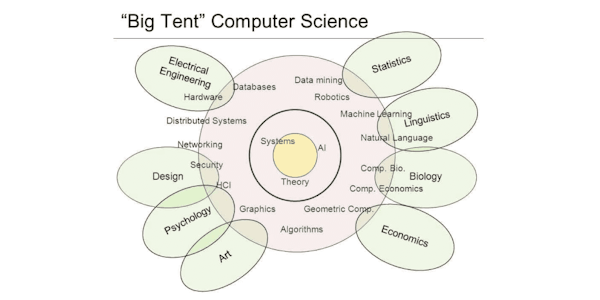
Geometry can be traced back to ancient Greece, but Computational Geometry evolved less than 40 years as a branch of computer science. The Computational Geometry taught in this course is derived from classical discrete/combinatorial geometry and modern computer science.
Computational Geometry first appeared on the horizon when M. I. Shamos presented his Ph.D. dissertation in 1978. Since then, this phrase has been used to refer to algorithmic study on discrete and combinatorial geometric structures and can also be regarded as the geometric version of Algorithm Design and Analysis. Computational Geometry is now considered the basis of robotics, computer aided design and manufacturing (CAM and CID), and geographic information systems (GIS).