With the hype surrounding large language models such as ChatGPT, I wondered whether I understood some of the basic concepts of machine learning (ML) algorithms. To my surprise, I realized there were a bunch of algorithms that I never really understood despite clearly using them in my sklearn workflow.

That’s when I decided to get my hands dirty with the mathematics behind machine learning. There are numerous resources on the web for mathematics such as MIT OCW, edX, Coursera’s Mathematics for Machine Learning Specialization, but most of them often lack depth and fail at bringing out mathematical intuition. Therefore, I was overjoyed when I came across Singular Value Decomposition by none other than Steve Brunton on the topic.

Introduction

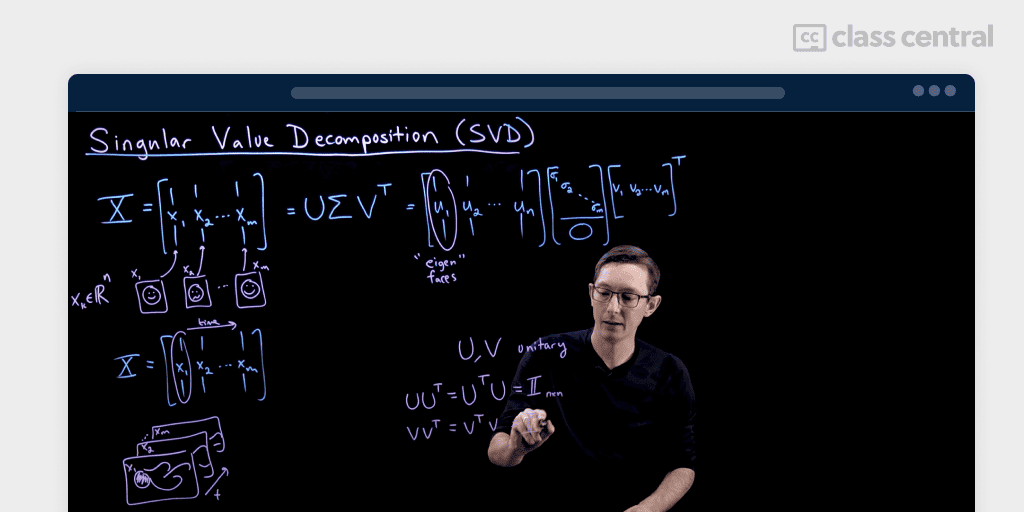
The course I found is a section from Steve Brunton’s Book Data Driven Science and Engineering.

Steve Brunton is an Adjunct Professor at the Department of Mechanical Engineering at the University of Washington. Having completed his Bachelor’s in Mathematics and a PhD in Aerospace Engineering from CalTech and Princeton, he is famous for applying ML techniques to areas such as fluid dynamics, dynamical systems, and control. The book covers topics from physics, control theory, signals, and machine learning, delving in-depth into the math behind the same.

What’s different about this course is that it’s completely open-sourced on his website, with a set of YouTube lectures and corresponding code on GitHub. It not only discusses the algorithm and its subsequent application but also provides proofs behind how the algorithm is adapted and modified mathematically and practically for each task! Professor Steve Brunton also goes out of his way to explain the codes for each application in Python and MATLAB.

If you are looking for an in-depth, intuitive, and practical experience to understand dimensionality reduction algorithms and its applications in machine learning, this is the best resource on the internet for the same.

Course

The course is structured as a series of 43 lectures. These are the topics roughly covered in the course:

• Introduction to Singular Value Decomposition (SVD)
• Image Compression using SVD
• Finding Moore-Penrose PseudoInverse using SVD
• Solving Linear System of Equations using SVD
• Least Squares Regression using SVD
• Linear Regression
• Principal Component Analysis (PCA)
• EigenFaces using PCA
• Optimal Rank Finding Optimal Rank in Low-Rank reduced Matrices in SVD
• Alignment Problem associated with using SVD
• Randomized SVD

Each section is laid out to first introduce the mathematical foundations, then build up to their application. The author first begins with an introduction to the SVD Algorithm, its properties such as dominant correlations, unitary matrices, and encourages you to ponder how to apply it, then moves straight ahead onto its application such as image compression. Another example of this wonderful flow would be how he discusses the mathematical properties of SVD and how it can be used to find inverse for non-square matrices called pseudoinverse. This makes the student ponder as to how one could use this wonderful new technique, then suddenly jumping to an obvious application such as regression or PCA.

Recommended Audience

This course is recommended for anyone who is interested in advancing their career in the field of ML/Deep Learning/AI as well as those interested in applying machine learning to applied physics research such as fluid dynamics, astrophysics, etc. A little linear algebra is required as the prerequisite.

How to Finish the Course Effectively

In order to effectively finish the course, I urge everyone to be patient. Patience is required if you want to understand the mathematical beauty behind the systems that we use. When you are discouraged or stuck, I urge the students to not give up but rather believe that Googling, using Math Stack Exchange or even talking to mentors and peers can genuinely help you out. Asking for help is the best thing one can do and solves the problem of “grit”.

Give yourself time and permission to fail at understanding some topics, ponder and revisit the material when you are stuck. Do not race along to reach your deadline. Please do not binge watch lectures as you won’t retain what you learn in your long-term memory. Spacing out videos each day consistently is recommended. For those who get bored midway through the course, I advise using a Pomodoro timer.

Taking notes is seriously recommended, especially to derive the proofs on your own. Do not skip any lecture or coding lecture as it will hinder your progress. It’s highly recommended to spend time thinking about how the algorithms can be applied.

Time

It took me approximately one month to finish the course. Given 43 lectures, one can complete it within a two month period if you have other commitments. It could take more than one month especially if you have problems with linear algebra basics.

Conclusion

I would highly recommend anyone who has problems understanding mathematics behind Machine Learning algorithms, especially dimensionality reduction, to take this course. It really has helped me understand a lot of other higher concepts as they have similarities with the SVD algorithm, and given me the confidence to take on more challenges to study mathematics.

I will probably take Steven Brunton’s course on Fourier Analysis or MIT OCW’s Multivariable Calculus next.

References

[1]Steven Brunton’s YouTube channel

[2] Chapter 1: Singular Value Decomposition | DATA DRIVEN SCIENCE & ENGINEERING (databookuw.com)

[3] Fourier Analysis: Overview

[4] MIT’s Course Review: Multivariable Calculus